Гомоскедастичность и гетероскедастичность временных рядов

В эконометрике и анализе временных рядов гомоскедастичность и гетероскедастичность — это ключевые характеристики, определяющие поведение дисперсии случайной ошибки модели.

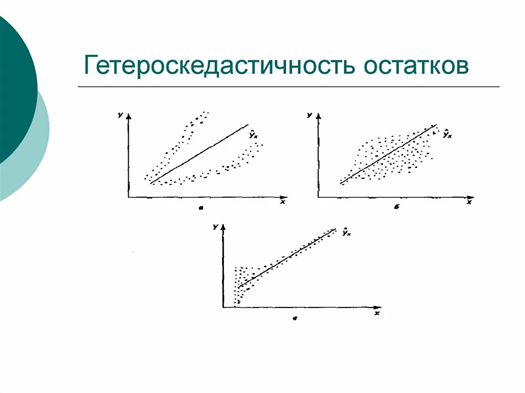
Понимание этих понятий критически важно при построении прогнозных моделей, особенно в таких областях, как финансовая аналитика, алгоритмическая торговля и риск-менеджмент.

Что означает гомоскедастичность

Гомоскедастичность означает, что дисперсия ошибок остается постоянной на протяжении всего временного ряда. Это идеальное состояние, при котором модель можно считать устойчивой и корректной в применении стандартных методов оценки, таких как метод наименьших квадратов. Когда выполняется условие Var(εₜ) = σ² = const, модель становится более предсказуемой, а результаты оценки — надежными. Гомоскедастичность упрощает интерпретацию коэффициентов и делает выводы статистически значимыми.

Отметим, что гомоскедастичность и гетероскедастичность, напротив, указывает на изменение дисперсии ошибок во времени. Это может выражаться в виде увеличения или снижения разброса ошибок в определенные периоды. В финансовых данных такое явление встречается часто, рынки нестабильны, и в периоды кризисов волатильность возрастает. Нарушение предпосылки постоянства дисперсии приводит к тому, что оценки параметров становятся смещенными и неэффективными, а доверительные интервалы — недостоверными. Для обнаружения гетероскедастичности используют тесты Бройша-Пагана, Уайта и Голдфелда-Квандта.

Если временной ряд демонстрирует гетероскедастичность, необходимо применять корректирующие методы. Одним из популярных решений являются модели ARCH и GARCH, которые адаптируются к изменяющейся дисперсии и позволяют более точно прогнозировать поведение переменных, особенно в условиях рыночной нестабильности.

Таким образом, различие между гомоскедастичностью и гетероскедастичностью не просто теоретическое — оно напрямую влияет на выбор аналитических инструментов и моделей. Игнорирование этих особенностей может привести к неверным выводам и повышенным рискам.

Поэтому грамотный квант-аналитик или финансовый специалист всегда проверяет свойства временного ряда перед построением прогноза и принимает соответствующие меры при выявлении гетероскедастичности. Контроль и корректный учет гетероскедастичности позволяют повысить точность прогнозов и снизить финансовые риски при принятии решений на основе временных рядов.